парашюты и парапланы| Главная » Статьи » Теория параплана » 3. Аэродинамика и аэромеханика ППС |
Силы, действующие на крыло
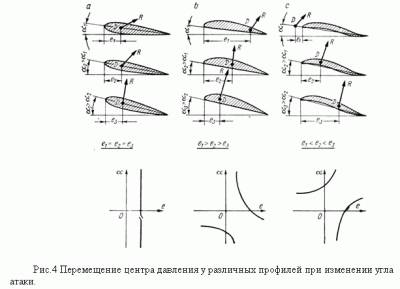
| По материалам работы [1]. Силы, действующие на крыло На рис.1 представлен профиль – сечение крыла, установленного под углом атаки α по отношению к потоку, набегающему на крыло со скоростью V. Хорду профиля обозначим b. 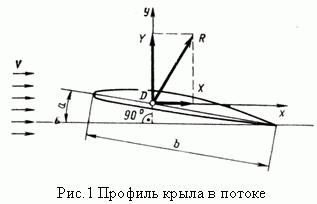 В скоростной системе координат полную аэродинамическую силу R, действующую на крыло, можно разложить на две составляющие: подъемную силу Y и силу лобового сопротивления X. Все эти три силы можно рассчитать по формулам: 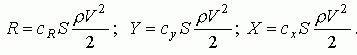 Здесь S – площадь крыла; cR, cy, cx – коэффициенты полной аэродинамической силы, аэродинамической подъемной силы, лобового сопротивления соответственно. Отметим, что в ГОСТе 20058-80, в скоростной системе координат эти коэффициенты обозначаются как cya, cxa. Аэродинамические коэффициенты, как функции от угла атаки для каждого профиля крыла получаются экспериментально, по результатам продувок моделей крыльев в аэродинамических трубах. На рис.2 показаны характерные зависимости для коэффициентов подъемной силы и силы лобового сопротивления от угла атаки [1]. Из рисунка 2 можно установить, что: 1) Для каждого профиля существует угол атаки α0, на котором подъемная сила равна нулю (угол нулевой подъемной силы). Для симметричного профиля угол нулевой подъемной силы также равен нулю. 2) Для каждого профиля существует угол атаки αкр, на котором подъемная сила достигает своего максимума. При превышении этого, критического угла атаки подъемная сила резко падает, что связано с нарушением плавного безотрывного обтекания профиля – срывом потока с крыла.  3) Коэффициент сопротивления крыла с данным профилем имеет наименьшее значение при угле атаки αcxmin. 4) Производная коэффициента аэродинамической подъемной силы по углу атаки: 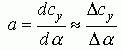 , определяет приращение коэффициента аэродинамической подъемной силы на единицу изменения угла атаки (наклон кривой). Чем больше величина a, тем интенсивнее приращение подъемной силы при изменении угла атаки (например, при входе системы в восходящий поток). Объединяя кривые для коэффициентов аэродинамической подъемной силы и силы лобового сопротивления от угла атаки в один график, можно получить поляру крыла первого рода, рис.3. На поляре производится разметка углов атаки, поскольку при объединении осей cy и cx, ось углов атаки исчезает. Нужно иметь в виду, что при использовании графиков 2 и 3, необходимо точно знать, как в каталоге профилей была определена хорда крыла, так как именно от нее измеряются углы атаки крыла. В большинстве случаев на хорде, как на основании, строятся верхняя и нижняя образующие профиля. Кроме величин аэродинамических коэффициентов, нужно знать также точку приложения полной аэродинамической силы R – центр давления (точка D на рис.1). В верхней части рисунка 4 показано положение полной аэродинамической силы для различных профилей на различных углах атаки, а в нижней части – изменение положения расстояния e центра давления (ЦД) от передней кромки профиля при изменении угла атаки. 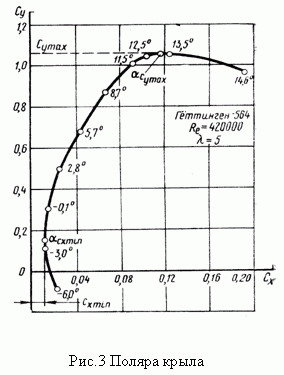  В первой колонке рисунка показан симметричный профиль – профиль с постоянным положением ЦД. Для данного профиля положение ЦД практически не изменяется, изменяется только модуль и направление вектора полной аэродинамической силы. Во второй колонке представлены несимметричные профили. У несимметричных профилей: двояковыпуклых, плосковыпуклых, выпукловогнутых, с ростом угла атаки ЦД перемещается вперед. Это профили с так называемым «нормальным» поведением ЦД. В третьей колонке представлены профили двойной кривизны (с S -образной средней линией), с несколько приподнятой кверху задней кромкой. С ростом угла атаки точка положения ЦД у них перемещается назад. Эти профили называются самобалансирующимися. Они находят широкое применение в летающих крыльях. Аэродинамический момент полной аэродинамической силы крыла относительно любой точки профиля, которой, например, может быть передняя кромка, рассчитывается по формуле: 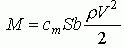 Здесь cm– коэффициент аэродинамического момента; b– хорда профиля, которой пропорционально плечо полной аэродинамической силы. Момент считается положительным, если направлен на увеличение угла атаки (передняя кромка профиля поднимается вверх) и наоборот. Из рисунка 4 видно, что с изменением угла атаки изменяется не только величина и направление вектора полной аэродинамической силы (он возрастает по модулю и поворачивается навстречу потоку), но и его плечо относительно передней кромки. Установлено, что на хорде профиля существует такая точка (фокус профиля), относительно которой момент полной аэродинамической силы почти постоянен в широком диапазоне углов атаки. Можно считать, что для большинства профилей в рабочем диапазоне углов атаки фокус лежит на 25% длины хорды профиля, считая от передней кромки. Коэффициент момента относительно фокуса обозначается cmF или cm0,25; по величине он равен коэффициенту момента относительно передней кромки профиля при cy=0: cmF=cm0. Для большинства профилей в справочниках приводится среднее значение cm0, поскольку оно практически постоянно. У профилей с нормальным перемещением ЦД (рис.4б), cm0– величина отрицательная, у профилей с обратным перемещением ЦД– положительная, а у симметричных профилей cm0=0. Момент полной аэродинамической силы относительно фокуса рассчитывается по формуле: 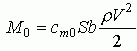 Анализируя перемещения ЦД у различных профилей, можно заключить, что действие аэродинамической силы, приложенной в ЦД профиля, эквивалентно действию этой же силы в фокусе профиля с учетом ее момента относительно фокуса (в соответствии с механическим принципом параллельного переноса сил). В практических расчетах лучше использовать неподвижный фокус вместо подвижного ЦД. При использовании справочных данных о величине аэродинамических коэффициентов очень важно знать, при каких условиях они были определены. Эти условия характеризуются прежде всего числом Рейнольдса, которое для малых высот полета может быть определено по формуле: 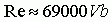 где размерности V[м/с], а b[м]. Аэродинамические коэффициенты cy, cx, cm профиля, измеренные при определенном числе Рейнольдса, могут надежно использоваться только для расчета крыла, которое работает при таком же числе Рейнольдса. В остальных случаях мы получаем лишь более или менее приближенные расчетные оценки. Литература 1. Яцек Капковский. Летающие крылья. Модели класса F-1A., М.:, Издательство ДОСААФ СССР, 1988., 127с. | |
| Просмотров: 6966 | Рейтинг: 5.0/1 |
| Всего комментариев: 0 | |
